在JavaScript开发者的开发生涯中的某些点,总会遇到奇怪的BUG——看似基础的数学问题,但却又觉得有些不对劲。总有一天,你会被告知JavaScript中的数字实际上是浮点数。试图了解浮点数和为什么他们如此奇怪,迎接你的将是一片又臭又长的文章。本文的目的是给JavaScript开发者简单讲解浮点数。
本文假设读者熟悉的用二进制表示的十进制数字(即1被写成1b,2是10b,3是11b,4是100b……等)。为了使文章表达的更清楚,在本章中,“十进制”主要是指计算机内部的十进制数字表示法(例如:2.718)。“二进制”在本文中指计算机内部的表示。书面陈述将分别被称为“以十为底″和“以二为底″。
浮点数
什么是浮点数,我们开始认为我们见过各种数字,我可可以说1是一个整数,因为它没有分数部分。
½被称为分数。这意味着,将一平均分开为二,分数是浮点运算中一个非常重要的概念。
0.5通常被称为一个十进制数。然而,有一个很重要的区别必须阐明——0.5实际上是分数½的十进制(以十为底)表示。本文中,我们将这种表示方法称为点表示法。我们把0.5称为有限表示(有限小数)因为其分数表示的数字是有限的——5后面没有其他数字。表示⅓的0.3333…是无限表示的例子。这个想法在我们的讨论非常重要。
还存在另一种表示全部整数,分数或小数的方法。你可能已经见过。它看起来像这样:6.022×1023(注:这是阿伏伽德罗数,这是摩尔的化学溶液中的分子的数目)。它通常被称为标准形式,或科学记数法。形式可以被抽象为像下面这样:
D1.D2D3D4...Dp x BE
这种通用形式被称作浮点数。
由p和D组成的序列——D1.D2D3D4...Dp——被称为有效数字或尾数。p是有效数字的权重,通常称为精度。有效数后的x是符号的一部分(本文中的乘法符号,将用*表示)。其后是基数,基数后是指数。该指数可以是正或负。
浮点数的好处是它可以用来表示任何数值。例如,整数1可以表示为1.0×10^0。光的速度可以表示为2.99792458×108 m/s。1/2可以被表示为二进制形式0.1×2^0。
移除小数点
在上面的例子中,我们仍然保留小数点(小数点在数字里面)。当用二进制表示数值的时候,这带来了一些问题。任意给定一个浮点数,比如π(PI),我们可以将其表示为一个浮点数:3.14159 x 100。用二进制表示,它看起来像这样:11.00100100 001111……假设在十六位机里表示数字,这意味着数字被放在机器里会是这样的:11001001000011111。现在的问题是:小数点应该放在哪里?这甚至不涉及指数(我们默认基数为2)。
如果数字变为5.14159?整数部分将变为101而不是11,增加了一位。当然,我们可以指定字段的前N位属于整数部分(即小数点的左边),其余属于小数部分,但那是另一篇关于定点数的话题。
一旦我们移除小数点后,我们只有两件东西需要记录:指数和尾数。我们可以通过应用变换公式将小数点移除,使广义浮点数看起来像这样:
D1D2D3D4...Dp / (Bp-1) x BE
这就是我们得到的大多数二进制浮点数。注意,现在有效数是一个整数。这使得它更易于存储一个浮点数在机器上。事实上,应用最广泛的二进制浮点数表示方法是IEEE 754标准。
IEEE 754
JavaScript中的浮点数采用IEEE-754格式的规定。更具体的说是一个双精度格式,这意味着每个浮点数占64位。虽然它不是二进制表示浮点数的唯一途径,但它是目前最广泛使用的格式。该格式用64位二进制表示像下面这样:
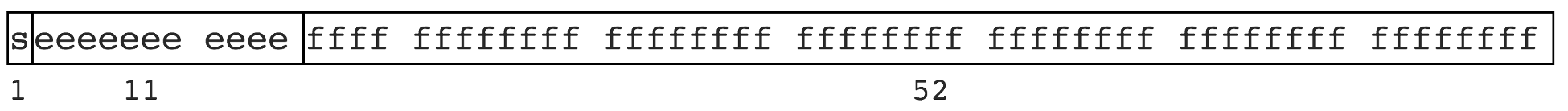
你可能注意到机器表示的方法和约定俗成的书面表示一点不同。在64位中,1位用于标志位——用来表示一个数是正数还是负数。11位用于指数–这允许指数最大到1024。剩下的52位代表的尾数。如果你曾经好奇为什么JavaScript中的某些东西如+0 和 -0,标志位说明一切——JavaScript中的所有数字都有符号位。Infinity和NaN也被编码进浮点数——2047作为一个特殊的指数。如果尾数是0,它是一个正无穷或负无限。如果不是,那么它是NaN。
舍入误差
有了上面对浮点数进行介绍,现在我们进入了一个更棘手的问题–舍入误差。它是所有开发者使用浮点数开发的祸根,JavaScript开发者尤其如此,因为JavaScript开发者唯一可用的编号格式是浮点数。
上面提到的分数⅓不能在以10为底中有限表示。这实际上在任何数制中都存在。例如,在在以二为底的数字中,1 / 10不能有限表示。被表示为0.00110011001100110011……注意0011是无限重复的。这是因为这个特别的怪癖,舍入误差造成的。
先看一个舍入误差的例子。考虑一个最著名的无理数,PI:3.141592653589793……大多数人记得前五位(3.1415)非常棒——我们将使用这个例子说明舍入误差,因此可以计算舍入误差:
(R - A) / Bp-1 ……其中`R`代表圆形的半径,`A`代表一个实数。`Bp`代表以`p`为底的精度。所以谨记PI的舍入误差:`0.00009265……`。
虽然这看起似乎不是很严重,让我们试着用以二为底的数来检验这个想法。考虑分数1 / 10。在十进制,它被写作0.1。在二进制中,它是:0.00011001100110011……假设我们仅保留5位尾数,可以写为0.0001。但0.0001在二进制表示法中实际是1 / 16(或0.0625)的表示!这意味着有舍入误差为0.0375,这是相当大的。想象一下基本的加法运算,如0.1 + 0.2,答案返回0.2625!
幸运的是,浮点规范指定ECMAScript最多使用52个尾数,所以舍入误差变得很小——规范的具体细节规避了大部分的舍入误差。因为对浮点数进行算术运算的过程中误差会被放大,IEEE 754规范还包括用于数学运算的具体算法。
然而,应该指出的是,尽管如此,算术运算的关联属性(比如加法,减法,乘法和减法)不能得到保证在处理浮点数时,即使精度再高。我的意思是,((x + y)+ A + B)不一定等于((x + y)+(A + B))。
这是JavaScript开发人员的祸根。例如,在JavaScript中,0.1 + 0.2 = = = 0.3将返回假。我希望你现在明白这是为什么。更糟的是,事实上,舍入误差会在连续的数学运算中增加(积累)。
在JavaScript处理浮点数
设计处理JavaScript数字的问题,已经存在很多的建议,好坏参半。大多数这些建议都是在算数运算之前或之后完成取舍。
到目前位置我见过的寥寥无几的建议就是把运算数全部存储为整数(无类型),然后格式化显示。通过一个例子可以看出,在账户中大量储存的美分而不是美元(不知道举的例子是什么账户)。这里有一个值得注意的问题——不是世界上所有的货币都是十进制的(毛里求斯币:毛里求斯卢比是毛里求斯共和国的流通货币。币值有25、50、100、200、500、1000和2000。辅币单位为分)。同时,吐槽了日元和人名币……。最终,你会重新创建浮点——有可能。
我见过处理浮点数最好的建议是使用库,像sinfuljs或mathjs。我个人比较喜欢mathjs(但实际上,任何和数学相关的我甚至不会使用JavaScript去做)。当需要任意精度数学计算的时候,BigDecimal也是非常有用的。
另一个被多次重复的建议是使用内置的toPrecision()和toFixed()方法。使用他们时最容易犯得逻辑错误是忘记这些方法的返回值字符串。所以如果你像下面这样会得不到想要的结果:
function foo(x, y) {
return x.toPrecision() + y.toPrecision()
}
> foo(0.1, 0.2)
"0.10.2"
设计内置方法toPrecision()和toFixed()的目的仅是用于显示。谨慎使用!
结论
JavaScript中的数字是真正的浮点数。由于二进制表示的固有缺陷,以及有限的机器空间,我们不得不面对一个充满舍入误差的规范。本文解释了为什么这些舍入误差是什么和为什么。记住使用一个很棒的库而不是自己去做一切。
注
原文:http://flippinawesome.org/2014/02/17/what-every-javascript-developer-should-know-about-floating-points/


